Los Poliedros Regulares

	Los Poliedros
1	Los poliedros regulares y sus elementos de simetría. Los cinco poliedros encajados unos dentro de otros.
1.1	El tetraedro tiene 7 ejes de rotación de dos tipos distintos y 6 planos de simetría.	Tetraedro		ggb
1.2	El cubo tiene 13 ejes de rotación de tres tipos distintos y 9 planos de simetría.	Cubo		ggb
1.3	Comparte los elementos de simetría del cubo aunque algunos cambian de función. Los que en el cubo pasan por vértices, en el octaedro pasan por los centros de las caras y viceversa.	Octaedro		ggb
1.4	El dodecaedro tiene 31 ejes de rotación y 15 planos de simetría.	Dodecaedro		ggb
1.5	El icosaedro comparte los elementos de simetría con el dodecaedro	Icosaedro		ggb
1.6	Los cinco poliedros regulares encajados uno dentro de otro	Omnipoliedro		ggb

	Truncamientos
2	Poliedros que se obtienen al cortar los regulares con planos perpendiculares las diagonales.
2.1	Cortamos los cuatro vértices del tetraedro con planos perpendiculares a los ejes de rotación.	Tetraedro truncado		ggb
2.2	Cortamos los ocho vértices del cubo con planos perpendiculares a las diagonales espaciales.	Cubo truncado		ggb
2.3	Cortamos los seis vértices del octaedro con planos perpendiculares a las diagonales espaciales.	Octaedro truncado		ggb
2.4	Cortamos los veinte vértices del dodecaedro con planos perpendiculares a las diagonales que unen vértices opuestos.	Dodecaedro truncado		ggb
2.5	Cortamos los doce vértices del icosaedro con planos perpendiculares a las diagonales que unen vértices opuestos	Icosaedro truncado		ggb
2.6	Se realizan dos tipos de cortes a un cubo, los que son perpendiculares a las diagonales espaciales y con planos perpendiculares a otros planos que pasan por aristas opuestas.	Pequeño Rombicuboctaaedro		ggb

	Poliedros estrellados
3	A cada cara de un poliedro le quitamos o le añadimos una pirámide
3.1	Formada por dos tetraedros. La intersección de los dos tetraedros es un octaedro.	Estrella octángula		ggb
3.2	Formado al expandir un cubo con las seis pirámides que unen cada una de sus caras con el centro. El poliedro tiene12 caras rómbicas que rellena el espacio.	Dodecaedro rómbico		ggb
3.3	Hacemos la simetría de las pirámides que unen cada cara triangular con el centro del octaedro. Cuando hacemos que las caras de las pirámides sean triángulos equiláteros, tenemos la estrella octángula.	Octaedro estrellado		ggb
3.4	Las pirámides de base pentagonal con el vértice en el centro del dodecaedro se llevan al exterior	Dodecaedro estrellado		ggb
3.5	Las pirámides de base triangular con el vértice en el centro del icosaaedro se llevan al exterior	Icosaedro estrellado		ggb

4	Relaciones entre poliedros
	Combinaciones con dos o más poliedros para dar lugar a otros nuevos.
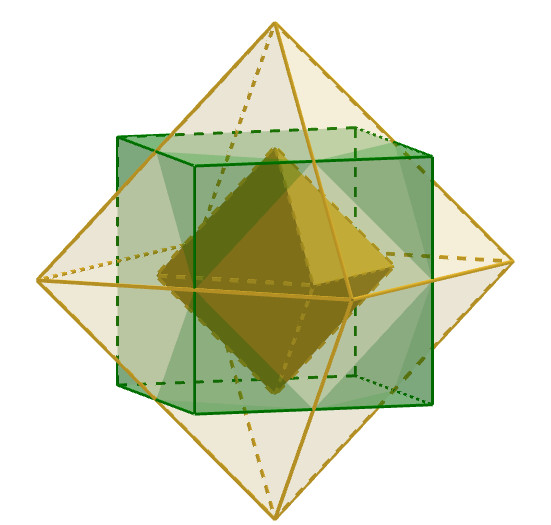
4.1	La relación entre el cubo y el octaedro. Las caras de uno son los vértices del otro y viceversa. Los dos tienen el mismo número de aristas	Dualidad		ggb
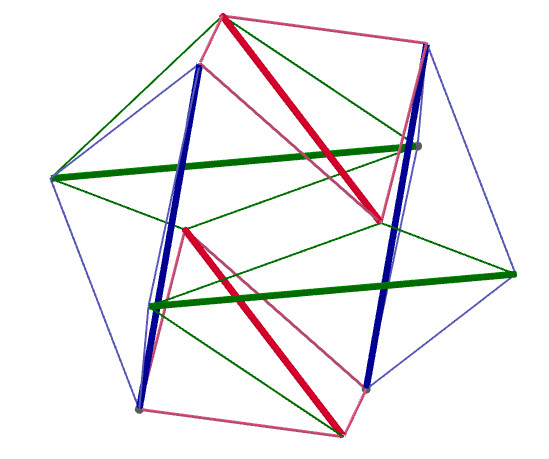
4.2	Algunas diagonales espaciales del icosaedro están en proporción áurea con su arista.	Icosaedro en el aire		ggb
4.3	Poliedro compuesto por un cubo y un octaedro cuyas aristas se cortan en los puntos medios.	Octaedro + Cubo		ggb
4.4	Poliedro compuesto por un dodecaedro y un icosaedro cuyas aristas se cortan en los puntos medios.	Dodecaedro+icosaedro		ggb
4.5	Las aristas del cubo se colocan sobre las diagonales de las caras del dodecaedro	Cinco cubos en un dodecaedro		ggb
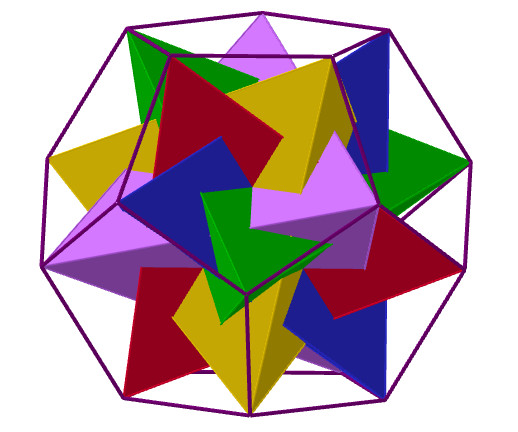
4.6	Las aristas de los tetraedros se colocan sobre las diagonales de los cubos de la aplicación anterior.	Cinco tetraedros en un dodecaedro		ggb
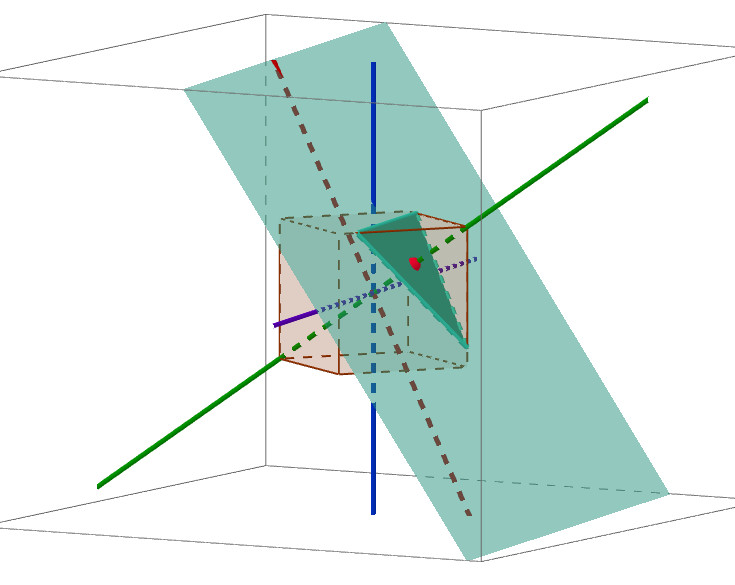
4.7	Cortes con planos perpendiculares a ciertas rectas para obtener polígonos como secciones en el cubo	Secciones planas del cubo		ggb