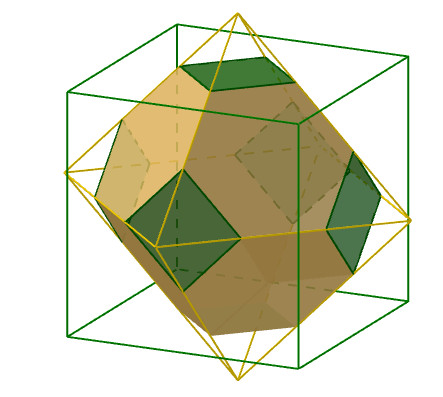
Poliedros truncados
| Ahora
vamos a coger un cubo y cortaremos en todas las esquinas una pequeña porción
de forma que la sección sea un triángulo equilátero.
El poliedro resultante es el cubo truncado que tiene catorce caras, ocho son los triángulos equiláteros que han surgido de los vértices, y las otras seis son octógonos que provienen de las caras del cubo a las que se han quitado los triángulos de las esquinas. En el applet java puedes ver los cortes que van desde el vértice al centro de la arista. ¿Cómo habrá que dar el corte para que todos los lados tengan la misma longitud?. |
|
Cuando los cortes llegan hasta el centro de cada arista, el poliedro que obtendremos es distinto a los demás, seguirá teniendo triángulos, pero los octógonos se convierten en cuadrados.
Aún podemos dar cortes más profundos en todas las caras y obtener nuevos poliedros truncados. Si los cortes pasan del centro de las aristas, los triángulos se convierten en otros polígonos. Estudia esta nueva situación.
Los
cortes podrían llegar hasta el centro de las caras. En ese momento los
truncamientos nos habrán llevado a otro de los sólidos platónicos: el
octaedro.
Realiza el proceso anterior partiendo del octaedro. Comienza con pequeños cortes en los vértices y hazlos más profundos poco a poco. Estudia los poliedros truncados que se obtienen